真值与内存的相互转换

概念定义

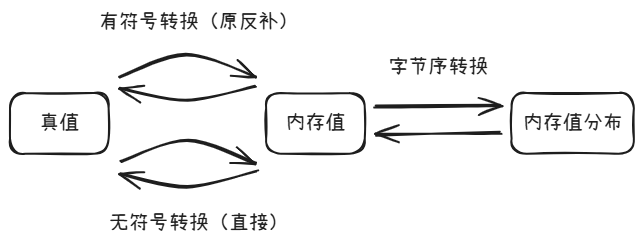
> 真值

实际意义上的值，比如代码里直接书写的值。

> 内存值

这个词是笔者自己造的，用于特指存储在内存中的值。笔者对这个概念还有如下规定或结论：

1. 内存值都是无符号的。
2. 习惯称“n进制内存值”为“内存n进制”，比如称“二进制内存值”为“内存二进制”。
3. 内存值与其对应的无符号真值是相等的。

> 内存值分布

这个词是笔者自己造的，用于表示内存值的各个字节在内存中的具体分布情况。

举例

有符号真值：

// 有符号十进制真值
-255

// 有符号二进制真值
-00000000 00000000 00000000 11111111(1,0000000 00000000 00000000 11111111)

// 有符号十六进制真值
-0x00 00 00 ff(0x80 00 00 ff)

经过有符号转换后，内存值为：

// 内存十进制
4294967041

// 内存二进制
11111111 11111111 11111111 00000001

// 内存十六进制
0xff ff ff 01

该内存值对应的内存值分布如下：

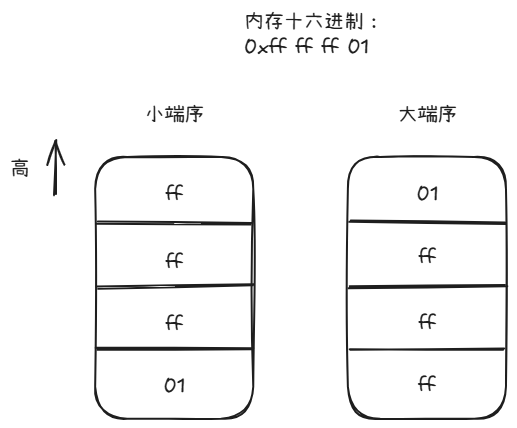
将上述内存值转换为无符号真值：

// 无符号十进制真值
4294967041

// 无符号二进制真值
11111111 11111111 11111111 00000001

// 无符号十六进制真值
0xff ff ff 01

补充说明

> 说明1

一般来说，编程语言和各种调试工具中，无法直接打印内存二进制（没有对应的格式说明符）；只能以无符号形式打印内存八进制、内存十六进制；可以以无符号或有符号形式打印内存十进制。

> 说明2

对于有符号十六进制真值 -0x00 00 00 ff，我们人类可以把负号写进去得到 0x80 00 00 ff，这看起来似乎是一样的。然而，在C语言中，以 %d 打印这两个数的输出结果是不一样的。

printf("%d\n", -0xff);  // -255
printf("%d\n", 0x800000ff); // -2147483393

详细分析：

关于常量的类型判断，可参考C11-6.4.4.1-Integer constants-ISO/IEC 9899:201x。

0xff 这个常量被存储为 int，其内存二进制为：

00000000 00000000 00000000 11111111

对它进行取负运算后，其内存二进制为：

11111111 11111111 11111111 00000001

%d 以有符号十进制形式打印该内存二进制，得到 -255：

11111111 11111111 11111111 00000001 ->
1,1111111 11111111 11111111 00000001 ->
1,0000000 00000000 00000000 11111110 ->
1,0000000 00000000 00000000 11111111 ->
-255

0x800000ff 这个常量会被当成一个正数，C尝试将其存储为 int，发现不够存，于是进一步尝试存储为 unsigned int，发现够存，于是该常量最终被存储为 unsigned int，其内存二进制为：

10000000 00000000 00000000 11111111

%d 以有符号十进制形式打印该内存二进制，得到 -2147483393：

10000000 00000000 00000000 11111111 ->
1,0000000 00000000 00000000 11111111 ->
1,1111111 11111111 11111111 00000000 ->
1,1111111 11111111 11111111 00000001 ->
-2147483393

关键在于：我们眼中的 0x800000ff 是一个负数，它等效于 -0x00 00 00 ff，但C语言会把它当成一个正数看待，然后使用存得下它的类型作为它的数据类型，换言之，在C语言中，-0x00 00 00 ff 的写法和 0x800000ff 的写法表示的完全是两个数。